Get instant access to this case solution for only $19
Laurinburg Precision Engineering Case Solution
It is vital to keep the following considerations in mind while choosing between coupon bonds and zero-coupon bonds. There are several elements that go into determining the price of a bond, including the profitability of the firm, the amount of time before the bond matures, the interest rate that is presently available on the market, and the price of the bond. They are required to undertake an examination into the organization's financial viability before to debating any of the topics stated on the agenda. This must be done before any of the items may be discussed. Coupon bonds are a superior choice that should be taken into consideration if the issuer is able to meet the obligations that have been made about the payment of interest in a timely manner. The company may want to consider purchasing zero-coupon bonds rather than standard ones to diversify its investment portfolio and possibly save money if the firm's financial position is not solid enough to provide for timely interest payments.
Following questions are answered in this case study solution
-
Using present value analysis estimate the number of zero coupon bonds(each with a face value of $1000) that will have to be offered to provide the $1 million Laurinburg Precision Engineering needs for expansion, if investors seek a yield of 10%. Assume interest will compound on a semiannual basis over the life of the five year bond issue.
-
Assume that McKinnon and MacDougald decide to issue coupon bonds to finance the expansion of Laurinburg Precision Engineering. The terms of the $1,000 bonds due January 15, 2009, specify an interest rate of 10% with semiannual compounding of interest payments. However, Shelia Cox is able to find a group of investors who will accept a yield of 8% interest. How much will the investors be willing to pay for the 10% bonds?
-
If zero-coupon bonds with semiannual compounding to be due January 15, 2009, are issued, what will be the amount due on that date if enough bonds are issued to provide $1 million on January 15, 2004, if the investors seek a yield of 8%?
-
How should Oliver MacKinnon and Beacham McDougald decide which bonds (the zero-coupon bonds or the 10% coupon bonds) to issue? What factors should they consider? Why?
Case Analysis for Laurinburg Precision Engineering
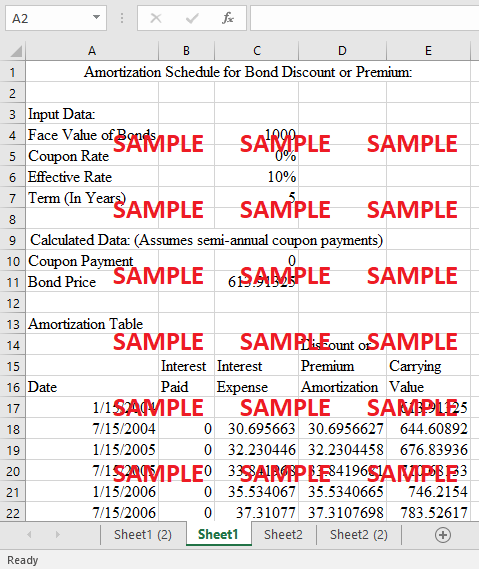
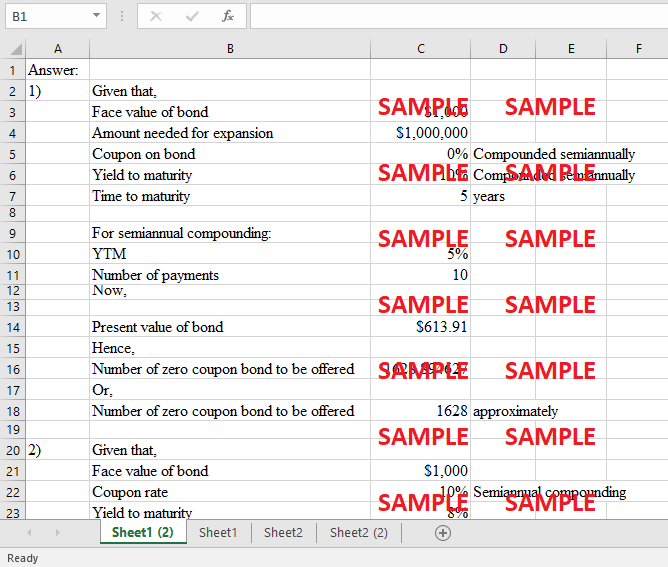
1. Using present value analysis estimate the number of zero-coupon bonds(each with a face value of $1000) that will have to be offered to provide the $1 million Laurinburg Precision Engineering needs for expansion, if investors seek a yield of 10%. Assume interest will compound on a semiannual basis over the life of the five-year bond issue.
|
Given that, |
|
|
|
Face value of bond |
$1,000 |
|
|
Amount needed for expansion |
$1,000,000 |
|
|
Coupon on bond |
0% |
Compounded semiannually |
|
Yield to maturity |
10% |
Compounded semiannually |
|
Time to maturity |
5 |
years |
|
|
|
|
|
For semiannual compounding: |
|
|
|
YTM |
5% |
|
|
Number of payments |
10 |
|
|
Now, |
|
|
|
|
|
|
|
Present value of bond |
$613.91 |
|
|
Hence, |
|
|
|
Number of zero-coupon bonds to be offered |
1628.894627 |
|
|
Or |
|
|
|
Number of zero-coupon bonds to be offered |
1628 |
approximately |
|
Amortization Schedule for Bond Discount or Premium: |
||||
|
|
|
|
|
|
|
Input Data: |
|
|
|
|
|
Face Value of Bonds |
|
1000 |
|
|
|
Coupon Rate |
|
0% |
|
|
|
Effective Rate |
|
10% |
|
|
|
Term (In Years) |
|
5 |
|
|
|
|
|
|
|
|
|
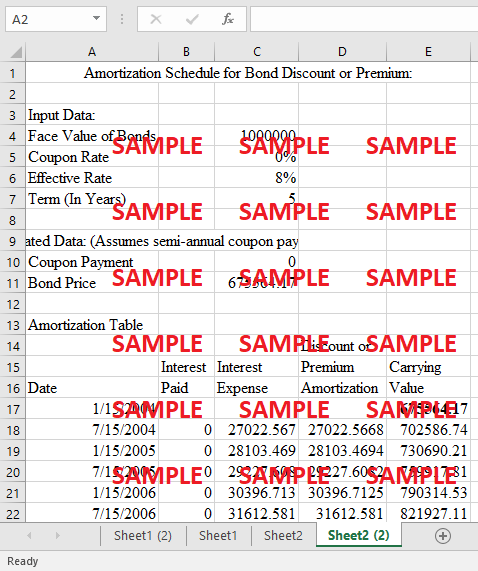
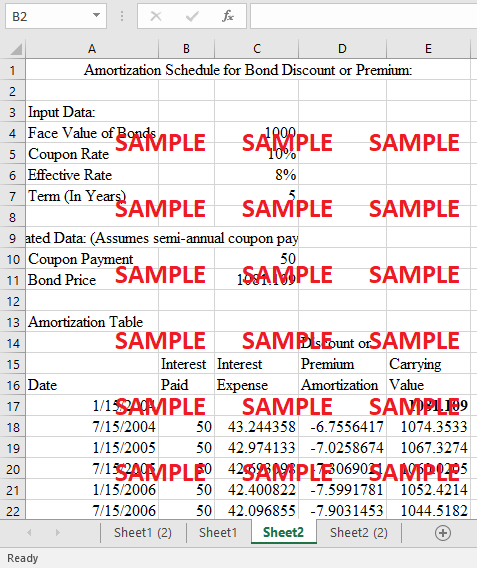
Calculated Data: (Assumes semi-annual coupon payments) |
|
|||
|
Coupon Payment |
|
0 |
|
|
|
Bond Price |
|
613.91325 |
|
|
|
|
|
|
|
|
|
Amortization Table |
|
|
|
|
|
|
|
|
Discount or |
|
|
|
Interest |
Interest |
Premium |
Carrying |
|
Date |
Paid |
Expense |
Amortization |
Value |
|
1/15/2004 |
|
|
|
613.91325 |
|
7/15/2004 |
0 |
30.695663 |
30.6956627 |
644.60892 |
|
1/15/2005 |
0 |
32.230446 |
32.2304458 |
676.83936 |
|
7/15/2005 |
0 |
33.841968 |
33.8419681 |
710.68133 |
|
1/15/2006 |
0 |
35.534067 |
35.5340665 |
746.2154 |
|
7/15/2006 |
0 |
37.31077 |
37.3107698 |
783.52617 |
|
1/15/2007 |
0 |
39.176308 |
39.1763083 |
822.70247 |
|
7/15/2007 |
0 |
41.135124 |
41.1351237 |
863.8376 |
|
1/15/2008 |
0 |
43.19188 |
43.1918799 |
907.02948 |
|
7/15/2008 |
0 |
45.351474 |
45.3514739 |
952.38095 |
|
1/15/2009 |
0 |
47.619048 |
47.6190476 |
1000 |
For a bond with a maturity of 5 years and an interest rate that is compounded semiannually and at 10%, the present value of the bond is
PV=1000/(1+0.05)^10 =613.91
It is necessary to sell a total of sixteen hundred twenty-nine bonds in order to bring in a total of one million dollars. You may make use of the following formula to get the answer to this question:
It works out to 1629 times (1000 minus 613.91), which results in a grand total of $628,940.61 being paid in interest fees.
This leads in a variance that, when added to the interest payment that is necessary for a pair bond at 10 percent, resulting in a total difference of $128,940.61 overall. This is because the unpaid interest on bonds with no coupons was carried over into the following year, which resulted in additional compound interest that needed to be paid at the end of the fifth year for bonds with no coupons. This was caused by the fact that the unpaid interest on bonds with no coupons was carried over into the next year. This is because the unpaid interest was carried over into the accounting for the next year, which is the reason why this occurred.
2. Assume that McKinnon and MacDougald decide to issue coupon bonds to finance the expansion of Laurinburg Precision Engineering. The terms of the $1,000 bonds due January 15, 2009, specify an interest rate of 10% with semiannual compounding of interest payments. However, Shelia Cox is able to find a group of investors who will accept a yield of 8% interest. How much will the investors be willing to pay for the 10% bonds?
Get instant access to this case solution for only $19
Get Instant Access to This Case Solution for Only $19
Standard Price
$25
Save $6 on your purchase
-$6
Amount to Pay
$19
Different Requirements? Order a Custom Solution
Calculate the Price
Related Case Solutions
Get More Out of This
Our essay writing services are the best in the world. If you are in search of a professional essay writer, place your order on our website.