Get instant access to this case solution for only $19
Seligram, Inc.: Electronic Testing Operations Case Solution
Seligram is a manufacturing company of defense related products. ETO is Seligram’s central testing division providing electrical and mechanical testing services for electric components such as circuits, diodes and transistors. ETO is a cost centre, and under the current accounting system, the costs of components testing are allocated based on direct labor cost. A company’s account manager and a consultant propose alternative methods, whereby separate pools are formed, and machine hours are used as a hand to allocate the costs that are not associated with direct labor. Pros and Cons analysis has been done, and calculations have been carried out to conclude that the consultant’s proposed plan is the best option as it allocates costs closest to the associated sources of costs.
Following questions are answered in this case study solution:
-
What caused the existing system at ETO to fail?
-
Calculate the reported costs of each of the five components under:
a. The existing system;
b. The system proposed by the accounting manager; and
c. The system proposed by the consultant.
-
Which system is preferable? Why?
-
Would you recommend any changes to the system you prefer? Why?
-
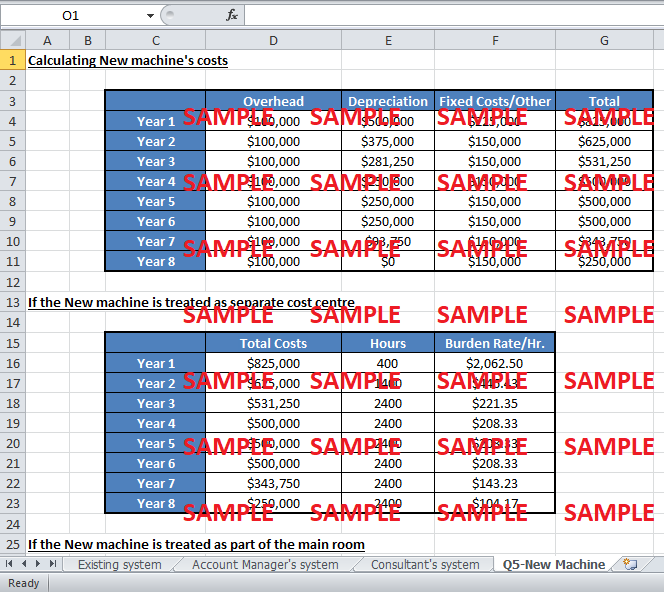
Would you treat the new machine as a separate cost center or as part of the main test room.?
Seligram Inc Electronic Testing Operations Case Analysis
1. What caused the existing system at ETO to fail?
The existing system at ETO failed because the burden rate was associated to direct labor costs incurred. Over the past years, there had been a decrease in the direct labor costs and a shift in the labor mix. The reasons for these changes were multifold; shift to the Just in Time inventory system, vendor certification that allows vendors to do the primary testing leaving ETO with only to test a small sample of each lot for verification purpose, increase in ETO’s engineering support to enhance customer experience, switch more complex testing methodologies. This reduced direct labor costs while increasing indirect costs such as personnel salaries and depreciation expenses. As the current processes underwent these changes in technology and innovation, the costing method was becoming more and more obsolete. Under the current costing method, the single cost pool could not provide detailed information of the allocation of the expenses. It worked under the assumption that all product lots used direct labor and overhead costs in the same proportion. It was not possible to determine which kinds of testing were allocated too little costs and which were allocated too much costs. Thus, the situation called for a new advanced method of accounting for the ETO.
2. Calculate the reported costs of each of the five components under:
The costs can be calculated under the three proposed systems using their different burden rates and costs pools.
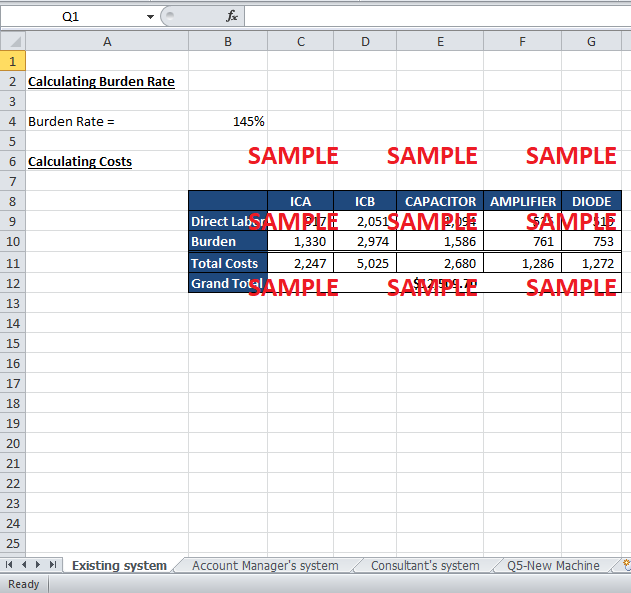
a. The existing system;
Under the current system, there is only one cost pool in which all the costs from the administrative, mechanical room and main electrical room are pooled in. The allocation base used for all three of them is direct labor. The cost of every object can be calculated by the costing formula:
Burden Rate = Total Overhead Costs / Total Direct Labor Costs
Cost Object = Direct Labor + (Burden Rate) (Direct Labor)
(Calculations have been done in the attached excel)
The total costs come out to be $ 12,510 under this existing system.
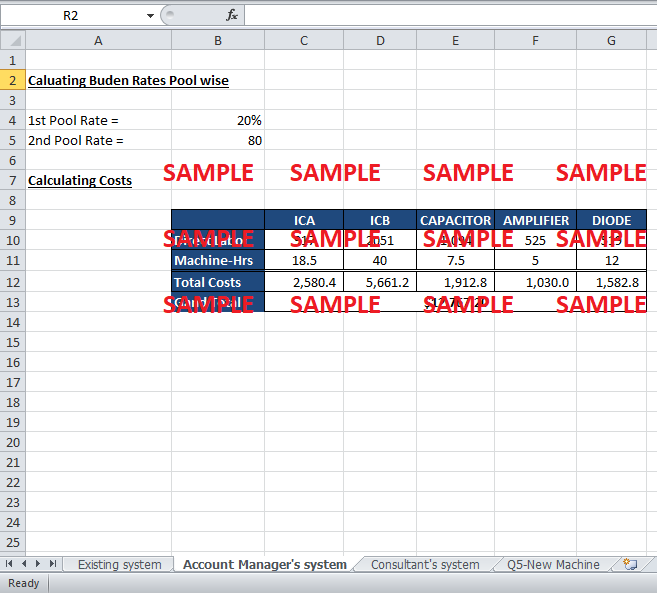
b. The system proposed by the accounting manager; and
Under this proposed system, there are two cost pools. Administrative and technical functions will be charged in one pool, and the burden rate for this pool would be based on direct labor per dollar. The other pool would comprise of all the other burden costs and will be charged based on machine hours. This is in order to separate the direct labor costs and charge them on the basis of labor costs while charging the administrative, engineering, technical, support and services staff on the basis of machine hours. The two separate pool’s burden rates can be calculated as follows:
1st Pool Rate = Administrative + Technical costs / Total Direct Labor Costs
2nd Pool Rate = other costs / Machine Hours
Cost Object = Direct Labor + (1st pool Rate) (Direct labor) + (2nd pool rate) (Hours used)
(Calculations have been done in the attached excel)
The total costs come out to be $ 12,767 under the account manager’s proposed accounting plan.
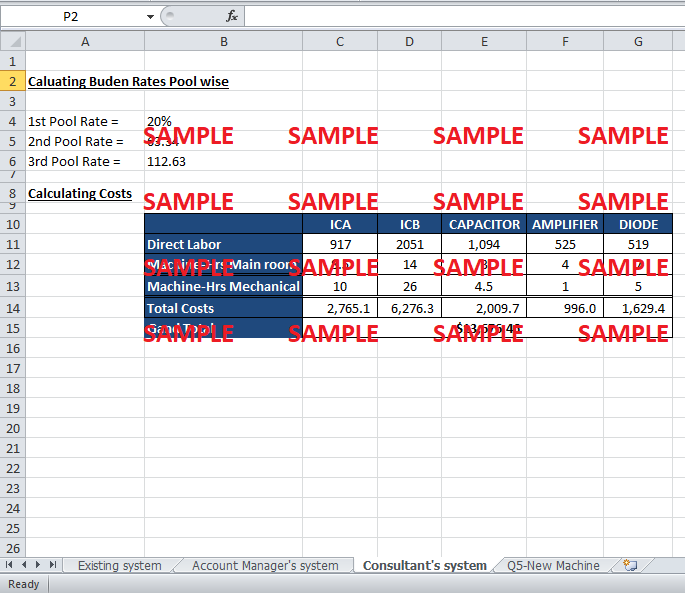
c. The system proposed by the consultant.
Under this system, there are three cost pools; the machine hours of the main test room and the mechanical test room will form separate pools. First pool, like in the previous plans, still contains the direct labor costs, while the rest of the administrative and technical costs have been separated as per their testing rooms and allocated according to the testing room’s machine hours.
1st Pool Rate = Administrative + Technical Costs / Total Direct Labor Costs
2nd Pool Rate = Main Room Costs / Main Room Machine Hours
3rd Pool Rate = Mechanical Room Costs / Mechanical Room Machine Hours
Cost Object = Direct Labor + (1st Pool Rate) (Direct Labor) + (2nd Pool Rate) (Main Room Hours used) + (3rd Pool Rate) (Mechanical Room hours used)
(Calculations have been done in the attached excel)
The total costs come out to be $ 13,676 in this case.
3. Which system is preferable? Why?
The pros and cons of each system can be weighed to find out which system is the best.
The current system’s positive points are only that it is a currently running system, a simple concept and has worked in the past for E.T.O; however, it has enormous cons like it allocates all the costs in the same proportion to all the components using only one cost pool and is getting more inaccurate and obsolete as the direct labor costs are decreasing with technological advancements.
If the Account Manager’s system is evaluated, its pros are that it uses separate allocation bases for labor and administrative/technical costs based on labor hours and machine hours respectively. Its cons are that it doesn’t have separate pools for separate testing rooms and doesn’t have a provision to cater for future machines.
As far as the Consultant’s system is concerned, the pros are separate cost pool for different cost kinds as well as testing rooms; however, one con of this system is that it shows the highest amount of total final costs value.
The best system can be either of the Account Manager’s and Consultant’s proposals, but the consultant’s system gets the advantage when it comes to accuracy. The consultant’s system allocates the costs accurately over cost kinds and the respective testing rooms; hence, it is the most preferable of the three systems.
4. Would you recommend any changes to the system you prefer? Why?
The consultant’s system, as evaluated to be the best of the three options above, allocates all costs to their relevant sources. There are no further changes recommended in this system as it already caters to all the requirements.
Get instant access to this case solution for only $19
Get Instant Access to This Case Solution for Only $19
Standard Price
$25
Save $6 on your purchase
-$6
Amount to Pay
$19
Different Requirements? Order a Custom Solution
Calculate the Price
Related Case Solutions
Get More Out of This
Our essay writing services are the best in the world. If you are in search of a professional essay writer, place your order on our website.