Get instant access to this case solution for only $19
Hamptonshire Express Case Solution
Products having a short shelf life might benefit from the one-period inventory model. They cannot be resold at a later point in time. The newsvendor model is the name given to this kind of business operation. Sheen had to get rid of any copies that didn't sell. Sheen then proceeded to determine her demand using the newsvendor approach. She predicted that daily demand for Express was regularly distributed, with a mean of 500 and a standard deviation of 100, based on data from comparable entrepreneurial operations and interviews with prospective Hamptonshire consumers. An accurate depiction of demand uncertainty must be developed to make inventory selections that optimize expected company profitability. When Armentrout didn't maximize his demand, Express ran out of stock, which reduced revenues for the company. Even though Armentrout still profited from his line, the inventory decrease ultimately led to lower sales.
Following questions are answered in this case study solution
-
How many Hamptonshire Express newspapers should Sheen stock?
-
How many hours should Sheen invest?
-
How many newspapers should Armentrout stock, etc.?
-
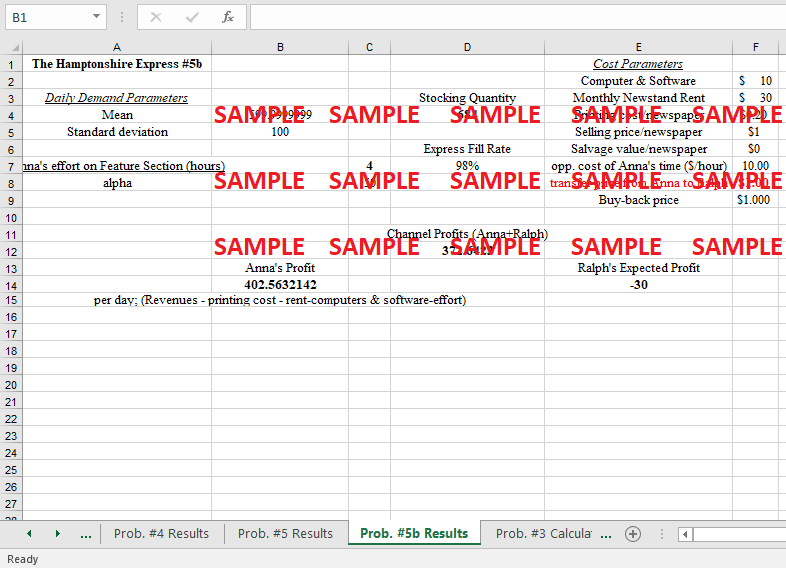
Given the new "Private Eye", how do Armentrout's decisions change?
-
How does the buyback price change Armentrout's stocking decision?
-
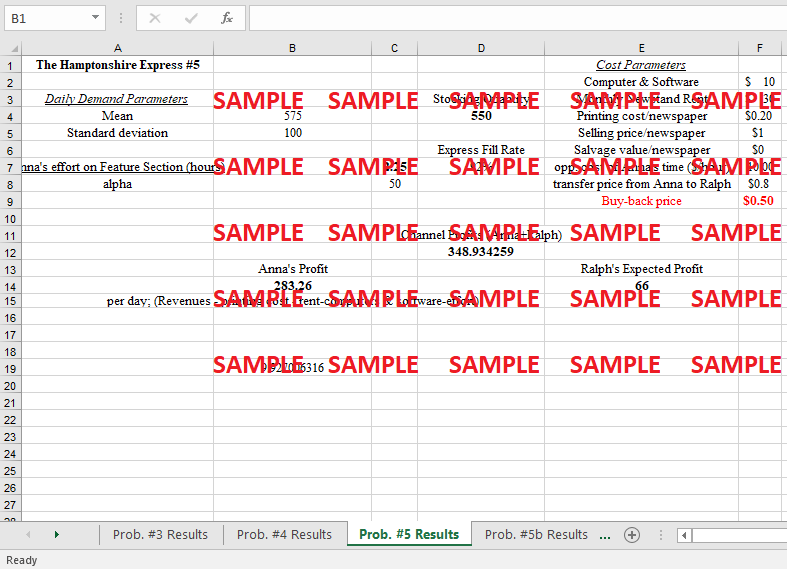
How would a VMI scheme influence Sheen and Armentrout's decisions?
Case Analysis for Hamptonshire Express
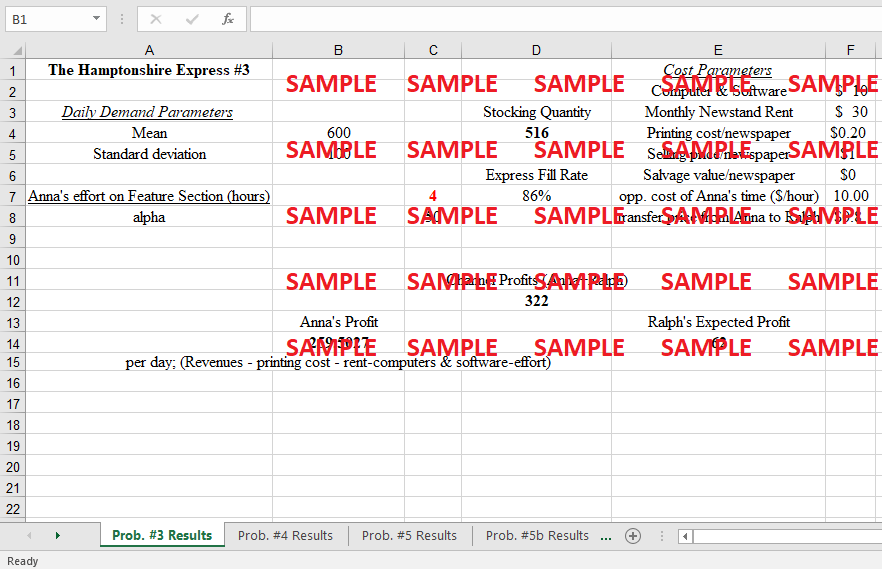
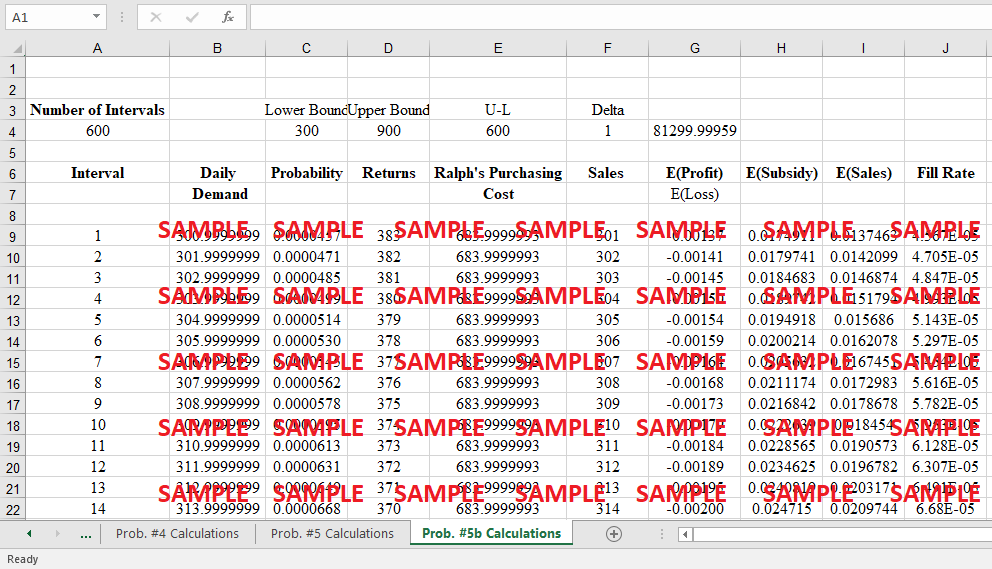
1. How many Hamptonshire Express newspapers should Sheen stock?
The underlying problem in the Hamptonshire Express case is that the demand for newspapers is erratic. To avoid product waste and financial losses, the sheen would have had to throw away all of her unsellable books. Even if Armentrout offered to purchase back the Express, Sheen was unsure whether she would accept. Armentrout's Express was completely out of stock. Because of this, buyers were forced to choose between buying the private line or not buying anything at all from the newsstand.
By varying the stocking quantity, the optimal stocking quantity was calculated to determine the maximum expected profit per day that could be made. The complete set of calculations is provided below.
Expected Demand = 500 = M. Standard deviation = s = 100. Marginal cost of production = 0.2 per copy and selling price per unit is 1.2. Any unsold copies are discarded. Hence the cost of understocking = Cu = 1.2 and Cost of Overstocking is Co = 0.2. The service level corresponding to optimal ordering is given by Cu / (Cu + Co) i.e., = 1.2/(1.2 + 0.2) = 85%. i.e. the optimal order quantity will be equal to the mean demand plus k times the standard deviation where k is the value of the curve as per the normal table. Looking up the normal table we get k = 1.07.
Hence quantity = 500 + 100*1.07 = 607 units.
Consequently, Sheen should stock approximately 607 units of newspapers. n. According to the following formula, this will result in the following amount of profit:
At this order quantity the Sales = 500 * 1.2 = $600. Cost = 607*0.2 + 10 + 30 = Cost of 607 units + Cost per day of leasing + Cost per day of rental = 161. Hence profit = Sales - Cost = 600 - 161 = $439.
To generate nearly $439 in profit, 607 units of newspapers must be purchased and stored.
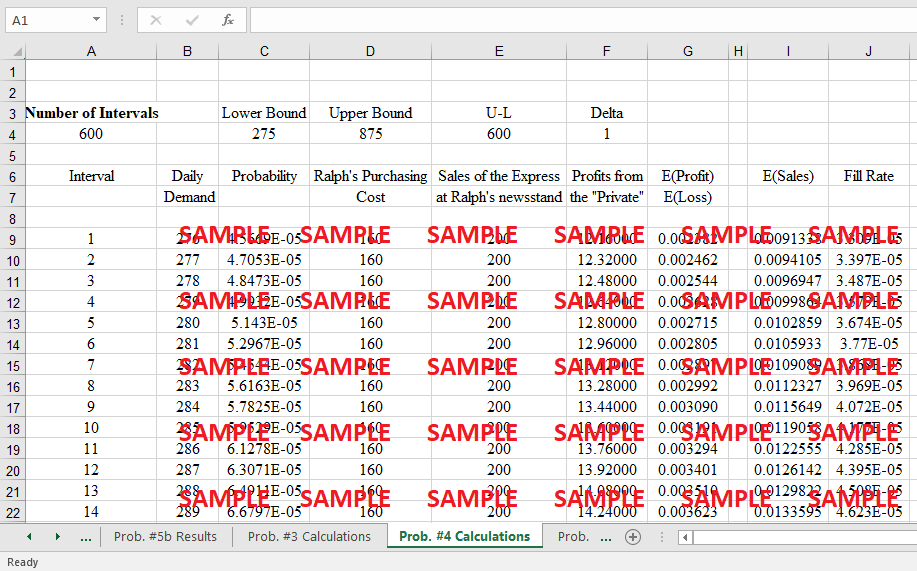
2. How many hours should Sheen invest?
Information provided: -
-
Rental cost for space = $ 10/day
-
Printing cost for newspaper = $ 0.2 /copy
-
Newsstand rental cost = $ 30/day
-
The selling price of a newspaper =$ 1/copy
-
Daily demand for the newspaper is normally distributed with a mean of 500 and a standard deviation of 100. (This means that demand varies from 400 to 600)
-
Demand is the function of time that the editor invest.
-
The editor records the time each day as per the given diagram. ( i,e at t=0 , D=500 , t=1 ,D= 550 , t =4 ,D =600)
-
Demand Function is given by D= 500 + 2 SQ ROOT(h)
-
Opportunity cost for working at another plane = $ 10 /Hr
Let us calculate the profit of the editor at D= 400,500,600
Profit = Total revenue - Total cost
When D=400,
Profit = (1*400 - (10+30+ 0.2*400) = (Price of 1 copy * total demand)- ((Rental cost of space + rental cost of newsstand) + Printing cost/copy * demand /day)
= $ 80
Similarly When D=5
Profit = (1*500 - (10+30 +0.2 *500) = 360
When D = 600
Profit = 440
From given Relation :
D=500 + 50 SR(h) h = ((D-500)/50)2
From above relation
At D= 400; h= 4 but this is not valid from given graph
At D=500; h= 0, but working hrs can not be zero
Get instant access to this case solution for only $19
Get Instant Access to This Case Solution for Only $19
Standard Price
$25
Save $6 on your purchase
-$6
Amount to Pay
$19
Different Requirements? Order a Custom Solution
Calculate the Price
Related Case Solutions
Get More Out of This
Our essay writing services are the best in the world. If you are in search of a professional essay writer, place your order on our website.