Get instant access to this case solution for only $19
Sampa Video Inc Case Solution
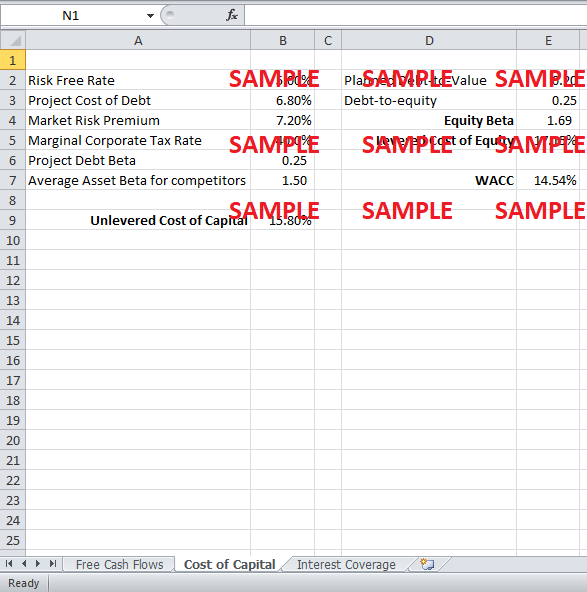
Assuming the firm was 100% equity financed, the cost of capital is calculated via the Capital Asset Pricing Model (CAPM). The equivalent beta for CAPM was taken to be the same as that of the competitors (Kramer.com and Cityretrive.com) which were 1.50. Using a Risk-free rate of 5% and a market premium of 7.2% the cost of capital comes out to be 15.80%.
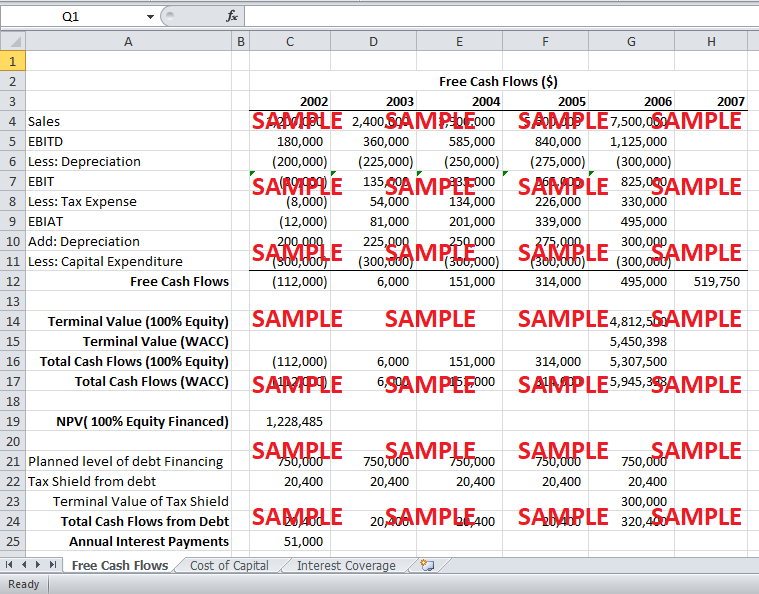
The annual projected cash flows were calculated as (EBIAT + Depreciation - CAPEX) and are shown in the attached excel file. The terminal value was calculated by the Gordon Growth Model, using the unlevered cost of capital, and the growth rate was assumed to be 5% as given in the Sampa Video case. The terminal value came out to be $4,812,500.
Following questions are answered in this case study solution:
-
What is the value of the project assuming the firm was 100% equity financed? What are the annual projected free cash flows? What discount rate is appropriate? (Sampa Video’s tax rate is 40%, see exhibit 2)
-
Value the project using the APV approach the firm raises $750,000 in debt to fund the project and keeps this amount of debt constant in perpetuity.
-
Value the project using the WACC approach assuming the firm maintains a constant 20% debt-to-market value ratio in perpetuity?
-
How do the values APV and WACC compare?
-
What are the end-of-year debt balances and interest payments implied by a 20% target debt-to-value ratio? Assume that the interest payments in year (t+1) depends on the debt at the end of year (t).
-
How does the project interest coverage from the policies in 2) and 3) compare with Sampa’s current interest coverage? (Let’s define interest coverage here as interest payments/EBITDA.)
-
What debt policy would you recommend that Sampa Video follows for this project (fixed debt amount or fixed leverage, and how much debt/leverage)? What is the project’s value under your chosen policy?
Sampa Video Case Analysis
Hence, discounting the projected cash flows at the unlevered cost of capital of 15.80% comes out to be $1,228,485 which means that the project will yield over a million dollars in profit discounted in today's dollars.
2. Value the project using the APV approach the firm raises $750,000 in debt to fund the project and keeps this amount of debt constant in perpetuity.
The adjusted present value approach assumes that equity and financing cash flows have different risks hence are discounted at different rates. In order to understand it in a simple way, APV valuation is equal to the present value of pure-equity cash flows plus side-effect cash flows of financing which can be positive and negative, as well if the cost of financial distress taken into account.
The annual tax shield from raising $750,000 in perpetuity comes out to be $20,400 and the terminal value of tax shields comes out to be $300,000. Hence the present value of tax shields, discounted at the cost of debt of 6.8%, from financing comes out to be $300,000.
Adding the side-effect cash flows of financing to the initial NPV of $1,228,485 gives us an APV of $1,528,485 implying that adding $750,000 of debt in perpetuity will increase the project's profitability by $300,000.
3. Value the project using the WACC approach assuming the firm maintains a constant 20% debt-to-market value ratio in perpetuity?
A planned debt-to-value of 20% implies a debt-to-equity ratio of 25%. By utilizing the below formula, the equity beta comes out to be 1.69.
β equity = β asset + (Debt / Equity)(1 - Marginal Tax rate)(β asset - β debt)
Using the levered equity beta, the cost of equity via the Capital Asset Pricing Model comes out to be 17.15 percent, which is higher as there has been added debt to the project which makes equity highly risky than if it were debt-free financed.
Hence, utilizing the above values, the Weighted Average Cost of Capital or WACC comes out to be 14.54%. This is lower than the cost of equity as debt is much cheaper than equity, and its proportional value drives down the WACC.
The terminal value was calculated by the Gordon Growth Model, using the weighted average cost of capital, and the growth rate was assumed to be 5% as given in the case. The terminal value comes out to be $5,450,398.
Hence, the NPV using the WACC approach comes out to be $1,706,017.
4. How do the values APV and WACC compare?
The level of debt financing in the APV approach is fixed at $750,000; hence, the interest tax shields are discounted at the cost of debt only as they bear no additional risk. However, if debt to a portion of the project value is fixed then the interest tax shields will also vary with the value of the project. Therefore, we discount the interest tax shields at the Weighted Average Cost of Capital to reflect the shared risk.
The Adjusted present value was $1,528,485 while the NPV from the WACC approach came out to be $1,706,017. The higher NPV from WACC does not necessarily mean that if someone utilizes the WACC approach and a debt-to-value of 20% that the project will be more profitable. It only reflects a difference in assumptions regarding working, and hence both approaches are not comparable in the strictest sense.
5. What are the end-of-year debt balances and interest payments implied by a 20% target debt-to-value ratio? Assume that the interest payments in year (t+1) depends on the debt at the end of year (t).
The end of the year debt balance implied by a 20% debt-to-value ratio is calculated via adding the initial investment of $1.5million to the NPV of $1,706,017 which yields the project value. The project value is then multiplied by the 20% target debt-to-value ratio and yields a debt balance of $641,203. By multiplying the debt balance by the cost-of-debt of 6.8% yields annual interest payments of $43,602. There has been assumed that the project value would remain constant over the years of its life.
6. How does the project interest coverage from the policies in 2) and 3) compare with Sampa's current interest coverage? (Let's define interest coverage here as interest payments/EBITDA.)
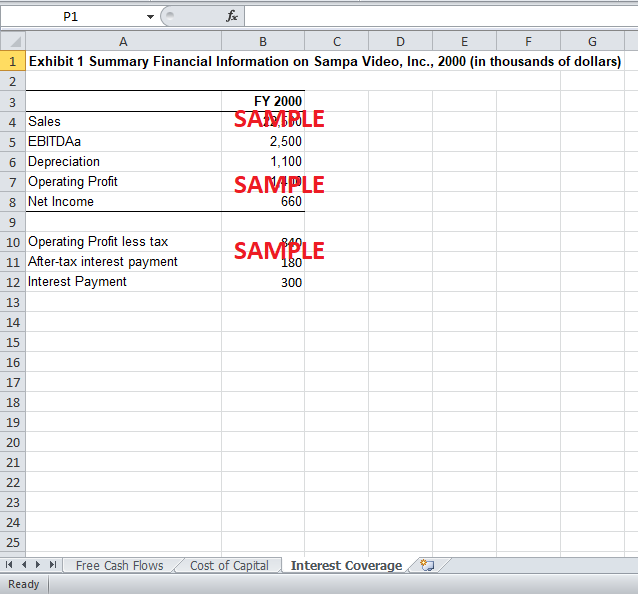
Currently, Sampa Video's interest payments come out to be $300,000 annually as can be seen in the excel sheet. Dividing the interest payments by the current EBITDA of $2.5million yields us an interest coverage ratio of 12%
If Sampa Video raises $750,000 in debt for the foreseeable future in perpetuity, then the interest coverage ratio for each of years is as follows:-
|
|
2002 |
2003 |
2004 |
2005 |
2006 |
|
Interest Coverage |
28.33% |
14.17% |
8.72% |
6.07% |
4.53% |
If Sampa video instead decides to keep a debt-to-value of 20% for the foreseeable future in perpetuity, then the interest coverage ratio for each of years is as follows:-
|
|
2002 |
2003 |
2004 |
2005 |
2006 |
|
Interest Coverage |
24.22% |
12.11% |
7.45% |
5.19% |
3.88% |
As it can be seen, the interest coverage ratio keeps decreasing as the years keep progressing simply because the EBITDA keeps on increasing as the project matures at the end of its life. Hence, both policies yield better interest coverage ratios near the end of the project life. However, in the initial stages, the project is extremely risky and yields interest coverage ratios of nearly double the current ratio implying that the project carries unnecessary risk in its inception. Hence, to counter-act the risk or to keep a level interest coverage ratio, the company might consider keeping a variable debt-to-value ratio throughout the life of the project so that it does not take on unnecessary debt, which will add to its project risk.
Get instant access to this case solution for only $19
Get Instant Access to This Case Solution for Only $19
Standard Price
$25
Save $6 on your purchase
-$6
Amount to Pay
$19
Different Requirements? Order a Custom Solution
Calculate the Price
Related Case Solutions
Get More Out of This
Our essay writing services are the best in the world. If you are in search of a professional essay writer, place your order on our website.